دانلود نرم افزار آزمایشگر صحت تابع غربال گر 100X^2+160X+59 نسبت به بخش پذیری

نرم افزار آزمایشگر صحت تابع غربال گر 100X^2+160X+59 نسبت به بخش پذیری نشان می دهد که هیچ کدام از خروجی های تابع مذکور به اعدادی با یکان (3) و یا اعدادی با یکان (7) بخش پذیر نبوده و خروجی های این تابع یا اعدادی اول بوده و یا فقط به اعدادی با یکان (9) و یا اعدادی با یکان (1) بخش پذیر می باشند که برای دانلود آن بر روی لینک زیر کلیک کنید.

لینک دانلود نرم افزار آزمایشگر

مقاله جدید تحلیلی درباره توابع غربال گر اعداد نسبت به بخش پذیری و کاربرد آنها در شناسایی و تحلیل ساختار پراکندگی اعداد اول

همه اعداد اول با توجه به مقادیر یکان آنها به جز اعداد (2 و 5) در چهار گروه عددی به صورت گروه اعداد اول دارای یکان (1) و گروه اعداد اول دارای یکان (3) و گروه اعداد اول دارای یکان (7) و گروه اعداد اول دارای یکان (9) دسته بندی می شوند که اگر بخواهیم برای تولید اعداد اول موجود در هر یک از چهار گروه عددی یاد شده توابعی را در نظر بگیریم متوجه خواهیم شد که توابع بدست آمده از این چهار گروه عددی بسیار شبیه به هم می باشند در حالی که پایه ساختاری توابع موجود در هریک از این گروه های عددی چهارگانه نسبت به توابع موجود در گروه های عددی چهارگانه دیگر اختلافی اساسی و بنیادین خواهد داشت و به عبارتی آنها هیچ ارتباطی با یکدیگر نخواهند داشت در حالی که در ریاضیات امروز به شدت تاکید می شود که باید برای همه اعداد اول دارای هر نوع یکان عددی یک تابع مشترک جهت تولید آنها را پیدا کرد که همین مسئله باعث می شود که ما هیچگاه نتوانیم درک صحیحی از اعداد اول و ساختار اعداد داشته باشیم و هرگاه که سعی می کنیم تا با تغییر ضرایب موجود در این گونه از توابع کارایی آن را بهبود ببخشیم در اصل به بخش دیگری از کارایی این توابع صدمه وارد کرده ایم زیرا همان طور که در ادامه این مقاله بررسی خواهیم کرد متوجه می شویم که با افزایش مقادیر ورودی به این نوع از توابع , اختلاف اعداد تولید شده خروجی از توابع موجود در هر یک از چهار گروه عددی چهارگانه با خروجی توابع دیگر گروه های عددی چهارگانه هم افزایش خواهد یافت و به عبارتی می توان گفت که توابع موجود در هر یک از گروه های عددی چهارگانه نسبت به توابع موجود در گروه های عددی چهارگانه دیگر مانند دو قطب هم نام آهنربا عمل کرده و از یکدیگر دور می شوند در حالی که در میان توابع موجود در یک گروه عددی چنین چیزی به طور کامل وجود ندارد و توابع زیادی در یک گروه عددی وجود دارند که همواره اختلاف اعداد خروجی آنها در صورت اعمال هر مقدار عدد ورودی یکسان به هر دو تابع , همواره عددی ثابت می باشد به طوری که حتی این امر نشان می دهد که احتمالا دیدگاه عمومی ما در مورد اعداد اول دوقلو هم باید اصلاح شود یعنی به جای اینکه بگوییم اعداد اول دوقلویی با یک واحد اختلاف در ساختار اعداد همواره موجود هستند باید بگوییم که اعداد اول دوقلویی با یک نوع یکان و با اختلافی مثلا 30 یا 60 یا 90 یا ... در ساختار اعداد بسیار فراوان و پایان ناپذیرند.

ما در این مقاله فقط در مورد دو گروه عددی اعداد اول یعنی گروه اعداد اول دارای یکان (9) و در خاتمه هم گروه اعداد اول دارای یکان (1) بحث می کنیم اما روش های به کار رفته در این مقاله را می توان برای دو گروه عددی دیگر یعنی گروه اعداد اول دارای یکان (3) و گروه اعداد اول دارای یکان (7) هم به استفاده کرد.

بنابراین در ابتدا جهت تحلیل ساختار و توابع اعداد اول موجود در گروه همه اعداد دارای یکان (9) داریم:

همه اعدادی که دارای یکان (9) می باشند یا اعدادی اول مانند {59,29,19,...} هستند که در گروه اعداد اول دارای یکان (9) قرار می گیرند و یا در صورت غیر اول بودن و تجزیه شدن هم مطابق قوانین مربوط به جدول ضرب فقط می توانند به یکی از سه حالت زیر و یا ترکیبی از آنها تجزیه شده باشند:

حالت اول: {اعدادی با یکان (3)} ضربدر {اعدادی با یکان (3)} مانند:

9 = 3 * 3

39 = 3 * 13

299 = 13 * 23

989 = 23 * 43

559 = 13 * 43

And …

حالت دوم: {اعدادی با یکان (7)} ضربدر {اعدادی با یکان (7)} مانند:

49 = 7 * 7

119 = 7 * 17

799 = 17 * 47

1369 = 37 * 37

1739 = 37 * 47

And …

حالت سوم: {اعدادی با یکان (1)} ضربدر {اعدادی با یکان (9)} مانند:

209 = 11 * 19

589 = 31 * 19

899 = 31 * 29

1829 = 31 * 59

2419 = 41 * 59

And …

در این مقاله به منظور آسان تر شدن بیان مفاهیم , حالت های اول و دوم و سوم را به اختصار به صورت زیر نامگذاری می کنیم:

حالت اول: {اعدادی با یکان (3)} ضربدر {اعدادی با یکان (3)} را در ادامه ی مقاله "مضارب (3*3)" می نامیم.

حالت دوم: {اعدادی با یکان (7)} ضربدر {اعدادی با یکان (7)} را در ادامه ی مقاله "مضارب (7*7)" می نامیم.

حالت سوم: {اعدادی با یکان (1)} ضربدر {اعدادی با یکان (9)} را در ادامه ی مقاله "مضارب (9*1)" می نامیم.

بنابراین با توجه به مطالب گفته شده چنانچه بتوان توسط روش هایی خاص اعدادی با یکان (9) را شناسایی کرد که این اعداد به هیچ وجه به هیچکدام از حالت های "مضارب (3*3)" و یا "مضارب (7*7)" و یا "مضارب (9*1)" تجزیه نشوند (البته به جز خود عدد و عدد یک) در این صورت اعداد شناسایی شده اعدادی اول خواهند بود که ما می خواهیم در ادامه این مقاله در ابتدا توسط روشی بسیار ساده و در عین حال قدرتمند صورت مسئله را ساده کرده و سپس به کمک این ساده سازی انجام گرفته و نتیجه گیری نهایی به توابعی جبری خواهیم رسید که این توابع می توانند اعدادی با یکان (9) را شناسایی کنند که به هیچ وجه به هیچکدام از "مضارب (3*3)" و یا "مضارب (7*7)" تجزیه نمی شوند و حتی با انتخاب صحیح اعداد ورودی به این توابع می توان خروجی هایی را تولید نمود که علاوه بر خاصیت عدم بخش پذیری به "مضارب (3*3)" و "مضارب (7*7)" دارای ویژگی عدم بخش پذیری به "مضارب (9*1)" هم بوده و در نتیجه همه اعداد تولید شده توسط این توابع اعدادی اول باشند.

برای انجام این بررسی حتما لازم است که ما بتوانیم تمامی اعداد و مضارب عددی را به صورت یک و یا چند قالب جبری پیاده سازی کنیم که برای این کار در ابتدا با استفاده از یک راه حل بسیار ساده و قدرتمند به نام روش تفکیک یکان عددی تمامی اعداد قابل کاربرد را در قالبی جبری به صورت زیر بیان می کنیم:

الف: تمامی اعداد با یکان (1) را به صورت عبارت جبری (10X + 1) بیان می کنیم.

ب: تمامی اعداد با یکان (3) را به صورت عبارت جبری (10X + 3) بیان می کنیم.

ج: تمامی اعداد با یکان (7) را به صورت عبارت جبری (10X + 7) بیان می کنیم.

د: تمامی اعداد با یکان (9) را به صورت عبارت جبری (10X + 9) بیان می کنیم.

پس حالا با توجه به عبارت های جبری بدست آمده ما می توانیم "مضارب (3*3)" و "مضارب (7*7)" و "مضارب (9*1)" را به صورت عبارت های جبری زیر بازنویسی کنیم:

 "مضارب (3*3)" برابر هستند با:

(10a + 3) * (10b + 3)  ===>  100ab + 30a + 30b + 9

"مضارب (7*7)" برابر هستند با:

(10a + 7) * (10b + 7)  ===>  100ab + 70a + 70b + 49

"مضارب (9*1)" برابر هستند با:

(10a + 1) * (10b + 9)  ===>  100ab + 90a + 10b + 9

همه عبارات جبری بالا در اصل می توانند تمامی اعداد بخش پذیر و غیر اول دارای یکان (9) را تولید کنند که در نتیجه ما می توانیم با دانستن این موضوع و استفاده از ویژگی مکمل های توابع (توابعی هستند که اعدادی را که تابع اصلی پوشش نمی دهند را پوشش می دهد) به توابعی دیگر دست پیدا کنیم که توابع مکمل بدست آمده درست برخلاف خود تابع اصلی فقط اعدادی را تولید می کنند که تابع اصلی نتوانسته است آنها را تولید کند و در نتیجه چنانچه عددی بتواند به طور مشترک در خروجی هر سه تابع مکمل تولید شود قطعا عدد بدست آمده عددی اول خواهد بود.

در توضیح بیشتر در مورد توابع مکمل بهتر است که دو مثال زیر را بررسی کنیم:

مثال اول: اگر ما بخواهیم برای کنترل یک بیماری , واکسنی را تولید کنیم قطعا از خود عامل بیماری زا استفاده کرده و با انجام تغییراتی بر روی این عامل بیماری زا مانند ضعیف کردن آن می توان به واکسن مورد نظر دست یافت.

مثال دوم: ما می دانیم که عبارت جبری 2X همواره اعدادی زوج را تولید می کند و به هیچ وجه نمی تواند اعدادی فرد را تولید کند به طوری که این اعداد فرد در حفره های میانی اعداد تولید شده زوج قرار گرفته اند , بنابراین ما جهت تولید اعداد فرد تولید نشده فقط کافی است که تابع مکمل تابع 2X را پیدا کنیم که برای این کار فقط کافی است از خود تابع 2X استفاده کرده و با اضافه کردن مقدار (e) به آن , تابع مکمل را به صورت 2X+(e) بدست آورد که به دلیل ساده بودن این تابع و درجه اول بودن آن فقط کافی است که (e) = 1 باشد و در نتیجه تابع 2X+(e) به صورت 2X+1 بازنویسی شود که این تابع مکمل می تواند تمامی اعدادی را که تابع اصلی نمی تواند تولید کند را تولید کند.

حالا با بررسی این سه عبارت جبری و بازنویسی شده متعلق به "مضارب (3*3)" و "مضارب (7*7)" و "مضارب (9*1)"و جایگذاری جداگانه عددی و رسم نمودار حاصل از این کار متوجه خواهیم شد قطعا در صورتی که مقادیر (a) و (b) را با هم مساوی بگیریم (به دلیل توزیعی که بر روی نمودار حاصله ایجاد شده و به طور کامل قابل اثبات است) می توانیم با اضافه کردن مقداری به نام (e) به توابع اصلی دقیقا توابع مکمل آنها را تولید کرد به طوری که مقدار (e) می تواند اعدادی ثابت و یا مقادیری جبری و کاملا مستقل برای هر یک از سه عبارت جبری یاد شده باشند و چون ما می خواهیم مکمل های توابع اصلی را که توابعی درجه دوم هستند را پیدا کنیم قطعا در اینجا فقط یک تابع مکمل نداشته بلکه دسته ای نامتناهی از توابع مکمل را خواهیم داشت و بنابراین مقادیر بسیار متنوعی از (e) را هم برای هر یک از عبارات جبری پیدا خواهیم نمود.

ما فعلا برای بدست آوردن مقادیر (e) نیازی به محاسبات پیچیده ریاضی نداریم بلکه به دلیل سادگی این عبارت جبری می توان از راه آماری و توسط یک برنامه ساده کامپیوتری (مانند کد منبع برنامه ای که در انتهای این مقاله آمده و به زبان C++ نوشته شده) هم این مقادیر را پیدا کرد به طوری که چنانچه نمونه های آماری ما برای آزمایش درستی مقادیر (e) تعدادی زیاد مثلا ده هزارتایی و در عین حال مقادیر (e) پیدا شده هم یک عبارت جبری ساده و درجه اول باشد می توان با توجه به نمودار رسم شده تا حد بسیار زیادی اطمینان داشت که مقادیر (e) پیدا شده مقادیری صحیح می باشند هر چند که یکی دیگر از راه های اثبات درست بودن مقدار (e) بدست آمده , اثبات نامساوی بوجود آمده میان تابع اصلی و توابع مکمل آن می باشد به طوری که مثلا فقط کافی است اثبات کنیم مانند نامساوی زیر , تابع مکمل پیدا شده همواره مخالف تابع اصلی می باشد:

100X^2 + 60X+ 9 + (e)  ≠  100ab + 30a + 30b + 9

پس با توجه به مطالب گفته شده و استفاده از نرم افزارهای یابنده مقادیر (e) ما معادلات زیر را خواهیم داشت:

صورت کلی توابع مکمل "مضارب (3*3)" برابر هستند با:

100ab + 30a + 30b + 9  ===>  100ab + 30a + 30b + 9 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 30(X) + 30(X) + 9 + (e)  ===>  100(X^2) + 60(X) + 9 + (e)

صورت کلی توابع مکمل "مضارب (7*7)" برابر هستند با:

100ab + 70a + 70b + 49  ===>  100ab + 70a + 70b + 49 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 70(X) + 70(X) + 49 + (e)  ===>  100(X^2) + 140(X) + 49 + (e)

صورت کلی توابع مکمل "مضارب (9*1)" برابر هستند با:

100ab + 90a + 10b + 9  ===>  100ab + 90a + 10b + 9 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 90(X) + 10(X) + 9 + (e)  ===> 100(X^2) + 100(X) + 9 + (e)

حالا با توجه به مطالب گفته شده , ما تعدادی از معادلات مکمل توابع "مضارب (3*3)" و توابع مکمل "مضارب (7*7)" را که با استفاده از یک برنامه ساده کامپیوتری یاد شده مقادیر (e) برای آنها مشخص شده است را به صورت زیر خواهیم داشت:

توابع مکمل "مضارب (3*3)" برابر هستند با:

100X^2 + 60X + 9 + (e)  ===>  (e) = 30X+10  ===>  100X^2 + 90X + 19

100X^2 + 60X + 9 + (e)  ===>  (e) = 50X+20  ===>  100X^2 + 110X + 29

100X^2 + 60X + 9 + (e)  ===>  (e) = 80X+20  ===>  100X^2 + 140X + 29

100X^2 + 60X + 9 + (e)  ===>  (e) = 100X+50  ===>  100X^2 + 160X + 59

100X^2 + 60X + 9 + (e)  ===>  (e) = 130X+50  ===>  100X^2 + 190X + 59

100X^2 + 60X + 9 + (e)  ===>  (e) = 130X+80  ===>  100X^2 + 190X + 89

100X^2 + 60X + 9 + (e)  ===>  (e) = 150X+70  ===>  100X^2 + 210X + 79

100X^2 + 60X + 9 + (e)  ===>  (e) = 150X+100  ===>  100X^2 + 210X + 109

100X^2 + 60X + 9 + (e)  ===>  (e) = 180X+10  ===>  100X^2 + 240X + 19

100X^2 + 60X + 9 + (e)  ===>  (e) = 180X+130  ===>  100X^2 + 240X + 139

And …

توابع مکمل "مضارب (7*7)" برابر هستند با:

100X^2 + 140X + 49 + (e)  ===>  (e) = 20X+10  ===>  100X^2 + 160X + 59

100X^2 + 140X + 49 + (e)  ===>  (e) = 50X+10  ===>  100X^2 + 190X + 59

100X^2 + 140X + 49 + (e)  ===>  (e) = 50X+40  ===>  100X^2 + 190X + 89

100X^2 + 140X + 49 + (e)  ===>  (e) = 70X+30  ===>  100X^2 + 210X + 79

100X^2 + 140X + 49 + (e)  ===>  (e) = 70X+60  ===>  100X^2 + 210X + 109

100X^2 + 140X + 49 + (e)  ===>  (e) = 100X+90  ===>  100X^2 + 240X + 139

100X^2 + 140X + 49 + (e)  ===>  (e) = 120X+40  ===>  100X^2 + 260X + 89

100X^2 + 140X + 49 + (e)  ===>  (e) = 120X+100  ===>  100X^2 + 260X + 149

100X^2 + 140X + 49 + (e)  ===>  (e) = 150X+10  ===>  100X^2 + 290X + 59

100X^2 + 140X + 49 + (e)  ===>  (e) = 150X+130  ===>  100X^2 + 290X + 179

And …

و در مورد توابع مکمل "مضارب (9*1)" هم باید گفت که متاسفانه به دلیل ساختار ویژه ای که "مضارب (9*1)" دارند هنوز نتوانسته ام که مقادیر مناسب (e) را برای این حالت پیدا کنم و ممکن است که این مقادیر به صورت یک عبارت جبری درجه بالا یا تابعی چند ضابطه ای و یا هر حالت منظم دیگری وجود داشته باشند.

با توجه به توابع مکمل "مضارب (3*3)" و توابع مکمل "مضارب (7*7)" به صورت یک نکته جالب و بسیار کاربردی خواهیم دید که تعداد زیادی از توابع مکمل مربوط به "مضارب (3*3)" و "مضارب (7*7)" دقیقا یکسان می باشند و این بدین معنی است که این دو مضرب در بیشتر ساختار عددی به صورت همنوا و هماهنگ حرکت می کنند و البته لازم به ذکر است که هرگز نباید این قضیه را با ساختار ناهماهنگ و در عین حال شبیه به یکدیگر توابع مکمل موجود در یک گروه عددی نسبت به توابع مکمل موجود در یک گروه عددی دیگر که در ابتدای مقاله راجع به آن گفته شد اشتباه کرد بلکه همان طور که گفته شد این شباهت فقط مربوط به ساختار درون هر گروه از گروه های چهارگانه عددی می باشد بنابراین ما می توانیم بسیاری از اعداد و حتی در مقاطع عددی بالاتر , تقریبا همه اعداد غیر قابل بخش پذیری به "مضارب (3*3)" و "مضارب (7*7)" را با استفاده از توابع مکمل مشترک بین این مضارب شناسایی کنیم و اگر بتوانیم مقادیر صحیح (e) را برای توابع مکمل "مضارب (9*1)" هم شناسایی کرده و توابع مکمل بدست آمده برای "مضارب (9*1)" را هم با این توابع مکمل مشترک دوباره مشترک کنیم در نتیجه توابع مکمل بدست آمده در اصل توابع مکمل برای هر سه حالت "مضارب (3*3)" و "مضارب (7*7)" و "مضارب (9*1)" بوده و همه اعداد خروجی این نوع از توابع به طور صد در صد اعدادی اول خواهند بود.

البته لازم به ذکر است که چون در حال حاضر مقادیر (e) مورد نظر برای توابع مکمل "مضارب (9*1)" شناسایی نشده است بنابراین می توان از راهکاری دیگر برای تولید اعداد اول توسط توابع مکمل مشترک بین "مضارب (3*3)" و "مضارب (7*7)" استفاده نمود که آن هم استفاده از مقادیر خاص ورودی به این گونه از توابع مکمل می باشد بدین صورت که چون تمامی اعداد خروجی از این توابع فقط ممکن است که به حالت "مضارب (9*1)" تقسیم پذیر باشند بنابراین می توان آنها را اعدادی با عوامل تجزیه کننده خالص در نظر گرفت و به همین دلیل قطعا روابط منظم ساختاری بسیاری در بین این اعداد شکل خواهد گرفت که با پیدا کردن این گونه از روابط می توان به هدف مورد نظر دست یافت. در حال حاضر هنوز نتوانسته ام این روابط را به طور کامل شناسایی کنم اما این گونه از روابط زمانی که ما ورودی هایی را به صورت مقادیری توانی در نظر بگیریم بسیار مشهود خواهند بود مثلا اگر برای تابع مکمل 100X^2+160X+59 ورودی هایی را به صورت (2^n) در نظر بگیریم خواهیم دید که یک نوع نظم ساختاری در بین مقادیر مختلف (n) به شرط اول بودن اعداد خروجی از این تابع دیده می شود که در حال حاضر هم سرگرم بررسی این نوع از روابط در بین مقادیر قابل قبول برای (n) می باشم.

تا این جا توابع مکمل مربوط به گروه اعداد اول دارای یکان (9) را بررسی کردیم و در ادامه این مقاله می خواهیم ساختار اعداد اول دوقلو را تحلیل کنیم اما جهت نمایش ساختار اعداد اول دوقلو لازم است که در ابتدا توابع مکمل مربوط به گروه اعداد اول دارای یکان (1) را هم مانند توابع مکمل مربوط به گروه اعداد اول دارای یکان (9)بررسی کنیم بدین صورت که در گروه همه اعداد دارای یکان (1) داریم:

همه اعدادی که دارای یکان (1) می باشند یا اعدادی اول مانند {41,31,11,...} هستند که در گروه اعداد اول دارای یکان (1) قرار می گیرند و یا در صورت غیر اول بودن و تجزیه شدن هم مطابق قوانین مربوط به جدول ضرب فقط می توانند به یکی از سه حالت زیر و یا ترکیبی از آنها تجزیه شده باشند:

حالت اول: {اعدادی با یکان (3)} ضربدر {اعدادی با یکان (7)} مانند:

21 = 3 * 7

221 = 13 * 17

111 = 3 * 37

481 = 13 * 37

851 = 23 * 37

And …

حالت دوم: {اعدادی با یکان (1)} ضربدر {اعدادی با یکان (1)} مانند:

121 = 11 * 11

341 = 11 * 31

451 = 11 * 41

1271 = 31 * 41

671 = 11 * 61

And …

حالت سوم: {اعدادی با یکان (9)} ضربدر {اعدادی با یکان (9)} مانند:

361 = 19 * 19

551 = 19 * 29

1711 = 29 * 59

1121 = 19 * 59

841 = 29 * 29

And …

در اینجا هم مانند قبل دوباره به منظور آسان تر شدن بیان مفاهیم , حالت های اول و دوم و سوم را به اختصار به صورت زیر نامگذاری می کنیم:

حالت اول: {اعدادی با یکان (3)} ضربدر {اعدادی با یکان (7)} را در ادامه ی مقاله "مضارب (7*3)" می نامیم.

حالت دوم: {اعدادی با یکان (1)} ضربدر {اعدادی با یکان (1)} را در ادامه ی مقاله "مضارب (1*1)" می نامیم.

حالت سوم: {اعدادی با یکان (9)} ضربدر {اعدادی با یکان (9)} را در ادامه ی مقاله "مضارب (9*9)" می نامیم.

پس با توجه به مضارب بدست آمده می توانیم "مضارب (7*3)" و "مضارب (1*1)" و "مضارب (9*9)" را به صورت عبارت های جبری زیر بازنویسی کنیم:

"مضارب (7*3)" برابر هستند با:

(10a + 3) * (10b + 7)  ===>  100ab + 70a + 30b + 21

"مضارب (1*1)" برابر هستند با:

(10a + 1) * (10b + 1)  ===>  100ab + 10a + 10b + 1

"مضارب (9*9)" برابر هستند با:

(10a + 9) * (10b + 9)  ===>  100ab + 90a + 90b + 81

حالا در حالت کلی توابع مکمل "مضارب (7*3)" و "مضارب (1*1)" و "مضارب (9*9)" مربوط به گروه اعداد اول دارای یکان (1) هم خواهیم داشت:

صورت کلی توابع مکمل "مضارب (7*3)" برابر هستند با:

100ab + 70a + 30b + 21  ===>  100ab + 70a + 30b + 21 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 70(X) + 30(X) + 21 + (e)  ===>  100(X^2) + 100(X) + 21 + (e)

صورت کلی توابع مکمل "مضارب (1*1)" برابر هستند با:

100ab + 10a + 10b + 1  ===>  100ab + 10a + 10b + 1 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 10(X) + 10(X) + 1 + (e)  ===>  100(X^2) + 20(X) + 1 + (e)

صورت کلی توابع مکمل "مضارب (9*9)" برابر هستند با:

100ab + 90a + 90b + 81  ===>  100ab + 90a + 90b + 81 + (e)  ===> a = b = X  ===>

===>  100(X)(X) + 90(X) + 90(X) + 81 + (e)  ===> 100(X^2) + 180(X) + 81 + (e)

و در نتیجه ما تعدادی از توابع مکمل "مضارب (7*3)" را که با استفاده از برنامه کامپیوتری یابنده (e) مقادیر (e) آنها مشخص شده است را به صورت زیر خواهیم داشت:

توابع مکمل "مضارب (7*3)" برابر هستند با:

100X^2 + 100X + 21 + (e)  ==>  (e) = 20X+10  ==>  100X^2 + 120X + 31

100X^2 + 100X + 21 + (e)  ==>  (e) = 30X+20  ==>  100X^2 + 130X + 41

100X^2 + 100X + 21 + (e)  ==>  (e) = 70X+20  ==>  100X^2 + 170X + 41

100X^2 + 100X + 21 + (e)  ==>  (e) = 70X+50  ==>  100X^2 + 170X + 71

100X^2 + 100X + 21 + (e)  ==>  (e) = 80X+40  ==>  100X^2 + 180X + 61

100X^2 + 100X + 21 + (e)  ==>  (e) = 120X+20  ==>  100X^2 + 220X + 41

100X^2 + 100X + 21 + (e)  ==>  (e) = 120X+80  ==>  100X^2 + 220X + 101

100X^2 + 100X + 21 + (e)  ==>  (e) = 130X+80  ==>  100X^2 + 230X + 101

100X^2 + 100X + 21 + (e)  ==>  (e) = 130X+110  ==>  100X^2 + 230X + 131

100X^2 + 100X + 21 + (e)  ==>  (e) = 170X+10  ==>  100X^2 + 270X + 31

And …

و در مورد توابع مکمل "مضارب (1*1)" و توابع مکمل "مضارب (9*9)" هم باید گفت که متاسفانه به دلیل ساختار ویژه ای که "مضارب (1*1)" و "مضارب (9*9)" دارند هنوز نتوانسته ام که مقادیر مناسب (e) را برای این دو حالت پیدا کنم و ممکن است که این مقادیر به صورت یک عبارت جبری درجه بالا یا تابعی چند ضابطه ای و یا هر حالت منظم دیگری وجود داشته باشند.

زمانی که توابع مکمل مشترک را بیشتر بررسی کنیم خواهیم دید که قضایای ریاضی بسیاری در بین آنها دیده می شود و حتی می توان توسط آنها ساختار های دیگر مربوط به قضایای اعداد اول و نظریه اعداد را هم تحلیل و یا اثبات نمود. به عنوان مثال دیده می شود که همه اعداد خروجی از این توابع در صورت تجزیه شدن به هیچ وجه به اعداد ورودی و یا ریشه های اعداد ورودی تقسیم نخواهند شد و این بدین معنی است که چنانچه عدد بسیار بزرگی که دارای ریشه های زیادی باشد و به عنوان ورودی به این توابع در نظر گرفته شود , احتمال اینکه عدد خروجی از این توابع عددی اول باشد بیشتر خواهد شد و همچنین دیده می شود که اعداد تقسیم کننده بیشتر به صورت جفت اعداد تقسیم کننده و با فاصله ای ثابت نسبت به یکدیگر در ساختار اعداد خروجی این توابع حرکت کرده و کار تقسیم را انجام می دهند که البته همه این قضایا نیاز به بررسی بیشتر و اثباتی محکم خواهند داشت و احتمالا اثبات آنها هم چندان سخت نخواهد بود.

اما همان طور که قبلا گفته شد یکی دیگر از کاربردهای توابع مکمل مربوط به تحلیل و نمایش چگونگی توزیع اعداد اول و اعداد اول دوقلو در ساختار اعداد می باشد بدین صورت که اگر به توابع مکمل مشترک بین "مضارب (3*3)" و "مضارب (7*7)" نگاهی بیندازیم خواهیم دید که مولفه میانی این توابع مکمل مشترک مقادیری به صورت 160X,190X,210X,240X,260X,290Xو... را دارا هستند در حالی که توابع مکمل "مضارب (7*3)" مولفه های میانی ای با مقادیری به صورت 120X,130X,170X,180X,220X,230Xو... را دارا هستند و همان طور که قبلا گفته شد میزان پوشش دهی تمامی این توابع به دلیل نامتناهی بودن تعداد آنها بسیار بالا بوده و تقریبا همه اعداد غیر قابل تقسیم پذیری به ضرایب مربوطه شان را می توانند تولید کنند و از طرفی می دانیم که همه اعداد اول موجود در دو گروه اعدادی با یکان (9) و اعدادی با یکان (1) حتما باید برای اول بودن به هیچ کدام از حالت های "مضارب (3*3)" و "مضارب (7*7)" و "مضارب (9*1)" و نیز "مضارب (7*3)" و "مضارب (1*1)" و "مضارب (9*9)" تجزیه پذیر نباشند پس در نتیجه تقریبا همه اعداد اول موجود در این دو گروه عددی باید از توابع مکمل مضارب یاد شده پیروی کنند و در نتیجه همانند مطلب گفته شده در ابتدای این مقاله , خواهیم دید که با افزایش مقادیر ورودی یکسان به توابع مکمل موجود در هر دو گروه عددی اختلاف خروجی های توابع مکمل هر گروه نسبت به گروه دیگر افزایش می یابد در حالی که در مورد توابع داخل هر گروه چنین حالتی به طور کامل پیش نمی آید و توابع مکمل زیادی در یک گروه عددی وجود خواهند داشت که اختلاف اعداد خروجی آنها همواره عددی ثابت خواهد بود. بنابراین احتمالا نگرش ما نسبت به ساختار واقعی اعداد اول دوقلو هم باید تغییر کند زیرا این قضیه نشان می دهد که روابط در بین اعداد موجود در گروه عددی دارای یکان (1) نسبت به گروه عددی دارای یکان (9) , تعداد اعداد اول دوقلویی که نسبت به هم دو واحد اختلاف دارند بسیار کم شده ولی در مقابل تعداد اعداد اول دوقلویی با یک نوع یکان عددی و به عبارتی هم گروه با یکدیگر که اختلاف عددی بین آنها ثابت و تقریبا به صورت مضربی از عدد 30 است به طور چشمگیری بسیار زیاد و احتمالا نامتناهی می باشد.

نتیجه گیری:

با توجه به مطالب گفته شده به این نتیجه می رسیم که روش بدست آمدن این توابع منطقی و در عین حال جدید می باشد و برخلاف آنچه که تصور می شود روش بدست آمدن این توابع از روی ساختار تابع تولید کننده اعداد اول اویلر و به طور کلی از توابع پلی نرمال مشتق نشده اند زیرا هرگز نمی توان با بسط دادن تابع اویلر و یا توابع پلی نرمال با هر نوع ضریب دلخواهی به تابعی کاملا دقیق برای تولید صد درصدی اعداد اول دست پیدا کرد چون تا زمانی که اعداد اول و توابع تولید کننده آنها در این چهار گروه عددی با هم یکسان فرض می شوند رسیدن به چنین خواسته ای بسیار مشکل و احتمالا محال خواهد بود.

البته برای درک بهتر مطالب گفته شده توصیه می شود که حتما نمودار تمامی حالت های ضرایب گفته شده رسم گردد بدین صورت که این نمودارها باید با ثابت نگه داشتن یکی از مقادیر (a) یا (b) و متغیر بودن مقدار دیگر رسم شود تا بتوان یکی از شگفتی های زیبای ساختاری اعداد یعنی وجود ساختارهای گل مانند با دوره تناوبی 100 تایی و ایجاد دروازه های خروجی اعداد اول در مرکز آنها را در نمودار حاصله مشاهده کرد و همچنین به دلایل وجود مقادیر اضافی (e) و چرایی مساوی بودن مقادیر (a) یا (b) در توابع مکمل که برای ثابت نمودن فاصله حرکت دو نمودار و جلوگیری از غیر قابل پیش بینی شدن وضعیت حرکتی و تداخل آنها نسبت به یکدیگر انجام می گیرد هم پی برد.

و همچنین امیدوارم که حداقل یکی از خوانندگان علاقه مند به این روش بتواند مقادیر (e) مورد نظر برای دیگر مضارب را هم پیدا کند تا با مشترک سازی توابع مکمل بدست آمده بتوان راهی صد درصد دقیق برای تولید اعداد اول در هر چهار گروه عددی را پیدا کرد.

در پایان از این که این مقاله را با وجود برخی ایرادات نگارشی موجود در آن مطالعه کردید متشکرم و در ضمن کد کوچک برنامه کامپیوتری یابنده مقادیر (e) را که به زبان (C++) نوشته شده و در این مقاله هم به آن اشاره شده است را می توانید در ذیل مشاهده نمایید:

//Finder (e) just for complement function 100X^2 + 60X + 9 common with complement function 100X^2 + 140X + 49

//Please change variables zz and ee for attain more complement function

//For up precision, Please change variables x and up this variables

//Store the complement function in text format to address "C:Finder(e).txt"

#include <iostream>

#include <conio.h>

#include <iomanip>

#include <fstream>

using namespace std;

int main(){

unsigned int y;

unsigned int k;

int z;

int x;

int p;

int ee;

int zz;

int f;

ofstream fout("C:\\Finder(e).txt");

x = 300;

for(zz = 0 ; zz < 500 ; zz=zz+10){

            for(ee = 0 ; ee < 500 ; ee=ee+10){

                        f = 0;

                        for(p = 0 ; p < x ; p++){

                                    y = (100*p*p)+(60*p)+9+(zz*p)+ee;

                                    for(k = 3 ; k < y ; k=k+10){

                                                z = y % k;

                                                if(z == 0){

                                                            f = 1;

                                                            k = y;

                                                            p = x;

                                                }

                                    }

                                    if(f == 0){

                                                y = (100*p*p)+(60*p)+9+(zz*p)+ee;

                                                for(k = 7 ; k < y ; k=k+10){

                                                            z = y % k;

                                                            if(z == 0){

                                                                        f = 1;

                                                                        k = y;

                                                                        p = x;

                                                            }

                                                }

                                    }

               }

               if(f == 0){

                                    cout << "(e) = " << zz << "X+" << ee << "    ===>   100X^2 + " << (zz+60) << "X + " << (ee+9) << endl << endl;

                                    fout << "(e) = " << zz << "X+" << ee << "    ===>   100X^2 + " << (zz+60) << "X + " << (ee+9) << endl << endl;

                        }

            }

}

cout << "===========================================" << endl;

cout << "END END END END END END END END END END END END END END " << endl << endl;

fout.close();

getch();

return 0;}

نویسنده و نظریه پرداز : حسین اختر محققی

تاریخ انتشار : 1392/7/21

جهت دانلود نسخه پی دی اف مقاله روی همین متن کلیک کنید

مقاله تصویری روشی ساده برای حل معادله X + Radical X = C

مقاله تصویری روشی ساده برای حل معادله

X + Radical X = C

مقاله روش تفکیک یکان عددی و تحلیل ساختار عددی موجود در قضیه آخر فرما

مقاله روش تفکیک یکان عددی و تحلیل ساختار عددی موجود در قضیه آخر فرما

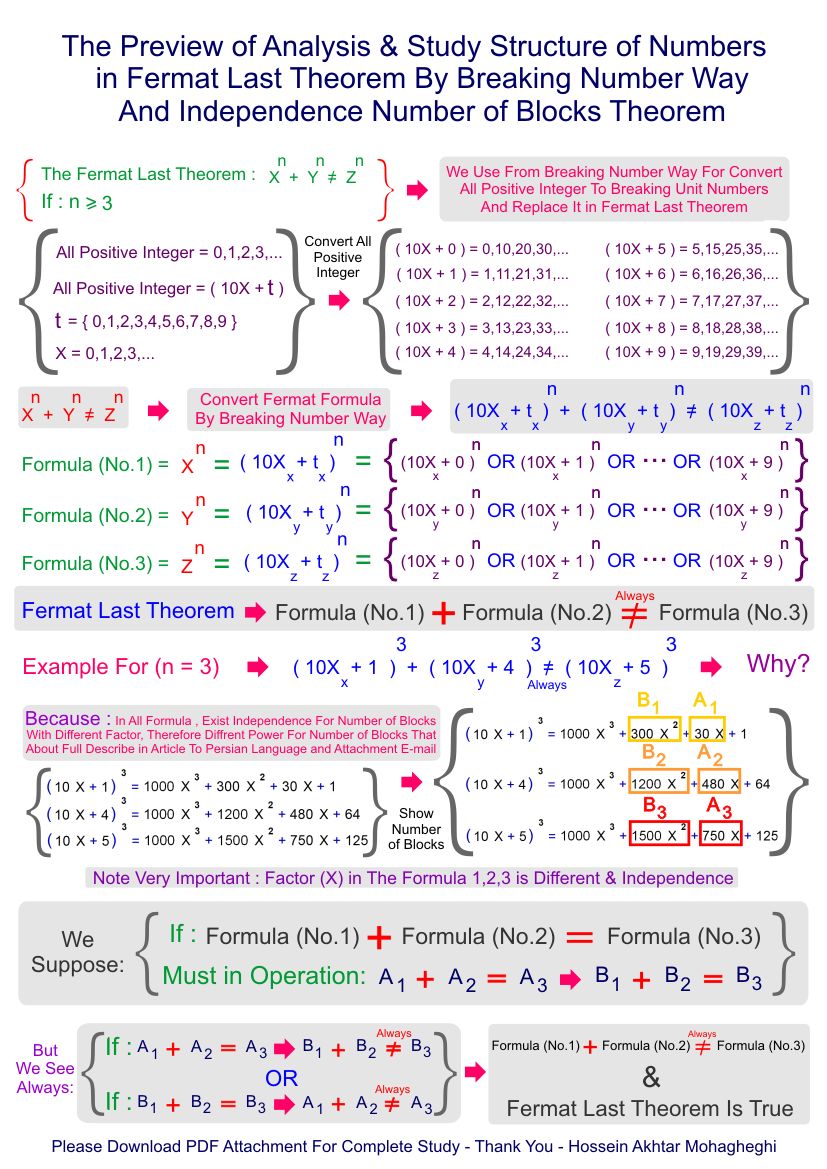
لطفا جهت دریافت فایل PDF مقاله تحلیل ساختار عددی قضیه آخر فرما اینجا را کلیک کنید

توابع غربال گر اعداد نسبت به بخش پذیری و کاربرد آنها در شناسایی اعداد اول

توابع غربال گر اعداد نسبت به بخش پذیری و کاربرد آنها در شناسایی اعداد اول

(توابع تولید کننده اعدادی با یک نوع مضرب و کاربردهای آن)

در تجزیه اعدادی که دارای یکانی برابر (9) هستند داریم :

factor (1000009)    ====>    293  *  3413

factor (1000019)    ====>    47  *  21277

factor (1000029)    ====>    3  *  31  *  10753

factor (1000039)    ====>    1000039

factor (1000049)    ====>    353  *  2833

factor (1000059)    ====>    3  *  17  *  19609

factor (1000069)    ====>    7  *  142867

factor (1000079)    ====>    281  *  3559

factor (1000089)    ====>    3  *  3  *  111121

factor (1000099)    ====>    1000099

نکته : اعدادی که نتیجه تجزیه آنها خود عدد اولیه می باشد اعدادی اول هستند و همچنین لازم به ذکر است که در این مقاله علامت (*) به معنی ضرب و علامت (^) به معنی توان می باشد. و همچنین در این مقاله گاهی اوقات به جای کلمه توابع از کلمه معادلات استفاده شده است که بهتر است از همان کلمه توابع استفاده شود.

همان طور که در مثال های بالا می بینید همواره اعدادی با یکان (9) یا اعدادی اول بوده و یا در صورت تجزیه شدن هم ممکن است که حداقل یکی از اعداد با یکان (3) مانند ( 3 و 13 و 23 و ...) و یا یکان (7) مانند (7 و 17 و 37 و ...) و یا یکان (1) مانند ( 11 و 31 و 41 و ...) و یا یکان (9) مانند ( 19 و 29 و 59 و ...) به عنوان ریشه اعداد در نتیجه حاصل از تجزیه آنها وجود داشته باشند.

حالا سئوال اینجاست که آیا یک و یا چند معادله جبری ساده وجود دارد که به کمک آنها بتوان اعدادی با یکان (9) را تولید کرد که آن اعداد تولید شده یا اعدادی اول بوده و یا در صورت تجزیه شدن هم فقط به اعدادی با یکان (1) مانند ( 11 و 31 و 41 و ...) و اعدادی با یکان (9) مانند ( 19 و 29 و 59 و ...) به عنوان ریشه اعداد تجزیه شوند؟ و یا به عبارتی همواره اعدادی با یکان (3) مانند ( 3 و 13 و 23 و ...) و اعدادی با یکان (7) مانند ( 7 و 17 و 37 و ...) به عنوان ریشه هیچ کدام از اعداد خروجی این معادلات وجود نداشته باشد و به نوعی این معادلات بتوانند به صورت یک مجموعه از معادلات غربال گر عددی رفتار کنند؟

جواب این سئوال به احتمال بسیار زیاد آری است و باید گفت که به تازگی توانسته ام توسط توسعه یک نوع روش نوین جبری در ریاضیات به نام روش تفکیک یکان عددی (برای آشنایی بیشتر با این روش به مقاله تحلیل ساختار عددی قضیه آخر فرما مراجعه شود) مجموعه ای بسیار بزرگ و احتمالا نامتناهی از معادلاتی تقریبا یک شکل و با یک قالب ساختاری را پیدا کنم که با توجه به پیش بینی هایی که این روش مبنی بر قطعیت وجود چنین معادلاتی در ساختار اعداد انجام می دهد و نیز وجود چندین نامعادله دائمی می توان انتظار داشت که این معادلات به ازای دامنه ورودی صفر تا بی نهایت همواره خروجی هایی با یکان (9) را تولید می کنند که یا اعدادی اول بوده و یا در صورت تجزیه شدن هم فقط می توانند به اعدادی با یکان (1) مانند ( 11 و 31 و 41 و ...) و اعدادی با یکان (9) مانند ( 19 و 29 و 59 و ...) به عنوان ریشه اعداد تجزیه شوند که در مثال زیر نمونه ای از خروجی های یکی از این معادلات را مشاهده می کنید که همگی آنها از شرایط ذکر شده تبعیت می کنند.

X  =  100    ====>     factor (1016059)    ====>    11  *  92369

X  =  101    ====>     factor (1036319)    ====>    1036319

X  =  102    ====>     factor (1056779)    ====>    1056779

X  =  103    ====>     factor (1077439)    ====>    11  *  41  *  2389

X  =  104    ====>     factor (1098299)    ====>    31  *  71  *  499

X  =  105    ====>     factor (1119359)    ====>    1119359

X  =  106    ====>     factor (1140619)    ====>    1140619

X  =  107    ====>     factor (1162079)    ====>    1162079

X  =  108    ====>     factor (1183739)    ====>    1183739

X  =  109    ====>     factor (1205599)    ====>    379  *  3181

همه مثال های بالا خروجی معادله (100*X^2)+(160*X)+(59) می باشند که این معادله به ازای تمام ورودی هایی از صفر تا ده هزار و نیز به صورت تصادفی و آماری با نمونه های بسیار فراوان و متنوع در بازه عددی ده هزار تا نه میلیون هم مورد آزمایش قرار گرفته است که تاکنون حتی یک مورد نقض هم در مورد خاصیت عدم بخش پذیری خروجی های آن به اعدادی با یکان (3) و یا اعدادی با یکان (7) مشاهده نشده است.

جهت آزمایش صحت این موضوع می توانید به نشانی های اینترنتی زیر مراجعه نمایید که لینک اول یک ماشین حساب اعداد صحیح بزرگ را نمایش می دهد که برای آزمایش باید از گزینه (Mod) آن استفاده نمایید و هرگز از گزینه تقسیم آن استفاده نکنید چون این ماشین حساب قسمت اعشاری تولید شده در تقسیم را نشان نمی دهد و لینک دوم هم مربوط به فاکتورگیری اعدادی تا 16 رقم می باشد که برای این کار باید عدد مورد نظر را بین دو پرانتز موجود در جلوی کلمه (factor) نوشته و سپس دکمه (Run) را کلیک نموده و نتیجه تجزیه عدد را مشاهده نمایید و لازم به ذکر است اعدادی که بین دو پرانتز نوشته می شوند نباید بیش از 16 رقم داشته باشند و بهتر است که اعداد حداکثر 15 رقم داشته باشند زیرا در غیر این صورت نرم افزار آن دچار خطا شده و نتایج اشتباهی را نشان می دهد مثلا وجود مضرب عدد (2) در جواب تجزیه اعداد فرد نشان دهنده خطا و انتخاب عدد بزرگ تر از ظرفیت نرم افزار است بنابراین برای اعداد 16 رقمی و بیشتر می توانید از همان لینک ماشین حساب و یا نرم افزارهای دیگری استفاده نمایید.

به منظور آسان تر شدن بررسی آماری این موضوع و خلاص شدن از انجام جمع و ضرب های متوالی می توانید توسط لینک سوم نرم افزاری ترکیبی تک منظوره که فقط جهت بررسی سریع تر و مطمئن تر اعداد خروجی معادله (100*X^2)+(160*X)+(59) تهیه کرده ام را دانلود نموده و به راحتی با تعیین بازه عددی مورد آزمایش از حداقل یک تا حداکثر نه میلیون و کلیک بر روی دکمه (شروع) و سپس کلیک بر روی دکمه (باز کردن) همان کار فاکتورگیری را به صورت دسته ای و بدون نیاز به هرگونه محاسبه و یا وارد کردن عددی و تنها با کلیک بر روی دکمه های (Run) موجود در صفحه باز شده انجام دهید و البته توصیه می شود که به منظور جلوگیری از زمان بری زیاد تولید اعداد توسط نرم افزار از بازه های عددی بیش از هزار تایی استفاده نشود.

1- لینک ماشین حساب اعداد صحیح بزرگ :

http://www.javascripter.net/math/calculators/100digitbigintcalculator.htm

2- لینک ماشین حساب تجزیه اعداد تا 16 رقم :

http://www.javascripter.net/math/primes/factorization.htm

3- لینک دانلود نرم افزار بررسی سریع و آماری تجزیه اعداد دربازه ورودی یک تا نه میلیون :

http://www.nerset.com/2/azmayeshgar/azmayeshgar.zip

همان طور که قبلا اشاره شد معادله (100*X^2)+(160*X)+(59) تنها یک نمونه از هزاران و شاید بی نهایت معادله ای است که دارای چنین ویژگی ای می باشند و به عنوان مثال تعداد دیگری از معادلاتی که به ازای ورودی صفر تا هزار و دویست صحت درستی آنها آزمایش شده و ممکن است که آنها هم دارای این ویژگی باشند عبارتند از :

( 100 * X ^ 2 ) + ( 90 * X ) + ( 19 )

( 100 * X ^ 2 ) + ( 110 * X ) + ( 29 )

( 100 * X ^ 2 ) + ( 140 * X ) + ( 29 )

( 100 * X ^ 2 ) + ( 160 * X ) + ( 59 )

( 100 * X ^ 2 ) + ( 190 * X ) + ( 59 )

( 100 * X ^ 2 ) + ( 190 * X ) + ( 89 )

( 100 * X ^ 2 ) + ( 210 * X ) + ( 79 )

( 100 * X ^ 2 ) + ( 210 * X ) + ( 109 )

( 100 * X ^ 2 ) + ( 240 * X ) + ( 19 )

( 100 * X ^ 2 ) + ( 240 * X ) + ( 139 )

( 100 * X ^ 2 ) + ( 260 * X ) + ( 89 )

( 100 * X ^ 2 ) + ( 260 * X ) + ( 149 )

( 100 * X ^ 2 ) + ( 290 * X ) + ( 59 )

( 100 * X ^ 2 ) + ( 290 * X ) + ( 179 )

( 100 * X ^ 2 ) + ( 290 * X ) + ( 209 )

( 100 * X ^ 2 ) + ( 310 * X ) + ( 89 )

( 100 * X ^ 2 ) + ( 310 * X ) + ( 209 )

( 100 * X ^ 2 ) + ( 310 * X ) + ( 239 )

( 100 * X ^ 2 ) + ( 340 * X ) + ( 209 )

( 100 * X ^ 2 ) + ( 340 * X ) + ( 269 )

( 100 * X ^ 2 ) + ( 360 * X ) + ( 199 )

( 100 * X ^ 2 ) + ( 360 * X ) + ( 319 )

( 100 * X ^ 2 ) + ( 390 * X ) + ( 229 )

( 100 * X ^ 2 ) + ( 390 * X ) + ( 349 )

( 100 * X ^ 2 ) + ( 390 * X ) + ( 379 )

( 100 * X ^ 2 ) + ( 410 * X ) + ( 269 )

( 100 * X ^ 2 ) + ( 410 * X ) + ( 389 )

( 100 * X ^ 2 ) + ( 410 * X ) + ( 419 )

( 100 * X ^ 2 ) + ( 440 * X ) + ( 359 )

( 100 * X ^ 2 ) + ( 440 * X ) + ( 479 )

همان طور که مشاهده می کنید این معادلات همگی دارای قالبی تقریبا یکسان بوده و همچنین می توان همگی آنها را در چهار دسته کلی از نظر ضریب مولفه میانی موجود در این معادلات که به صورت کلی برابر با 90X , 110X , 140X , 160X , 190X و ... می باشند دسته بندی نمود و چون این معادلات بخش بسیار بزرگی از اعداد دارای یکان (9) را به طور کامل نسبت به وجود اعدادی که به اعداد اولی با یکان (3) و یکان (7) بخش پذیر هستند را غربال می کند آنها را معادلات غربال گر (3*3) و (7*7) می نامیم.

مهمترین کاربرد این معادلات در این است که چنانچه با تغییراتی در ساختار آنها و یا پیدا کردن راهی جهت انتخاب ورودی ها به این معادلات بتوان خروجی هایی را تولید کرد که علاوه بر ویژگی های قبلی به جز خود عدد (1) به هیچ وجه به هیچ کدام از اعداد با یکان (1) مانند ( 11 و 21 و 31 و ...) و به خصوص اعدادی با یکان (1) که از حاصل ضرب اعدادی با یکان (9) در هم مانند ( 551 = 19 * 29) بوجود می آیند  , بخش پذیر نباشند در این صورت تمامی خروجی های آنها اعدادی اول خواهند بود که البته روش ایجاد تغییرات در ساختار معادلات برای رسیدن به چنین منظوری چندان مناسب نیست چون در صورتی که ساختار اولیه معادلات تغییر کند به احتمال زیاد خاصیت قبلی خود ( عدم بخش پذیری خروجی های معادله به اعدادی با یکان (3) مانند ( 3 و 13 و 23 و ...) و اعدادی با یکان (7) مانند ( 7 و 17 و 37 و ...) را از دست خواهند داد و بنابراین تنها راه باقیمانده روش انتخاب گزینشی اعداد ورودی به معادله می باشد و اگر چه می توان حالت های گوناگونی را برای این کار در نظر گرفت اما یکی از حالت های جالب برای این کار استفاده از مقادیر A به توان n است (A ^ n) که می تواند به عنوان ورودی معادلات در نظر گرفته شود مثلا اگر برای معادله (100*X^2)+(160*X)+(59) ورودی هایی به صورت مقدار 2 به توان n یعنی همان ( 2 ^ n ) را داشته باشیم که در آن متغیر n برابر با اعدادی نظیر 27 , 97 , 267 , 287 , 797 , 1287 , 2817 و ... باشد در این صورت تمامی خروجی های ایجاد شده عددی اول خواهند بود و با کمی دقت بر روی اعداد نامبرده و به خصوص اعداد 27 , 287 , 2817 خواهیم دید که یک نوع نظم ساختاری در بین این اعداد وجود دارد که با پی بردن به این نظم احتمالا می توان اعداد بعدی را هم بدون آزمایش اول بودن اعداد حاصل از معادله پیدا کرد ولی برای یافتن چنین نظمی نیاز به انجام بررسی های فراوان بوسیله شبکه ای از هزاران کامپیوتر قدرتمند برای داشتن توان محاسباتی بالا می باشد که در حال حاضر چنین امکانی برایم موجود نیست ولی احتمالا بتوان در آینده حتی بدون نیاز به چنین قدرت محاسباتی بالایی و فقط به کمک روابط جدید ریاضی این مشکل را هم حل نموده و بدین ترتیب به راحتی اعداد فوق بزرگ اول با یکان (9) را شناسایی نمود.

لازم به ذکر است که این نوع از معادلات غربال گر فقط محدود به ساختار اعدادی با یکان (9) نمی شوند بلکه در ساختار اعدادی با یکان (1) هم معادلاتی با همین قالب موجود بوده که همه خروجی های اینگونه از معادلات با وجود اینکه دارای یکان (1) می باشند و طبق قوانین جدول ضرب هم باید بخش بزرگی از اعدادی که دارای یکان (1) می باشند به اعدادی با یکان (3) و نیز اعدادی با یکان (7) بخش پذیر باشند ولی هیچکدام از اعداد خروجی این معادلات به اعدادی با یکان (3) و یا اعدادی با یکان (7) بخش پذیر نمی باشند و بنابراین اعداد خروجی این معادلات یا اعدادی اول بوده و یا فقط به اعدادی با یکان (1) و یا اعدادی با یکان (9) بخش پذیر می باشند و برخی از این معادلات که به ازای ورودی صفر تا هزار و دویست صحت درستی آنها آزمایش شده و ممکن است که آنها هم دارای این ویژگی باشند عبارتند از :

( 100 * X ^ 2 ) + ( 120 * X ) + ( 31 )

( 100 * X ^ 2 ) + ( 130 * X ) + ( 41 )

( 100 * X ^ 2 ) + ( 170 * X ) + ( 41 )

( 100 * X ^ 2 ) + ( 170 * X ) + ( 71 )

( 100 * X ^ 2 ) + ( 180 * X ) + ( 61 )

( 100 * X ^ 2 ) + ( 220 * X ) + ( 41 )

( 100 * X ^ 2 ) + ( 220 * X ) + ( 101 )

( 100 * X ^ 2 ) + ( 230 * X ) + ( 101 )

( 100 * X ^ 2 ) + ( 230 * X ) + ( 131 )

( 100 * X ^ 2 ) + ( 270 * X ) + ( 31 )

( 100 * X ^ 2 ) + ( 270 * X ) + ( 151 )

( 100 * X ^ 2 ) + ( 270 * X ) + ( 181 )

( 100 * X ^ 2 ) + ( 280 * X ) + ( 71 )

( 100 * X ^ 2 ) + ( 280 * X ) + ( 191 )

( 100 * X ^ 2 ) + ( 320 * X ) + ( 131 )

( 100 * X ^ 2 ) + ( 320 * X ) + ( 251 )

( 100 * X ^ 2 ) + ( 330 * X ) + ( 121 )

( 100 * X ^ 2 ) + ( 330 * X ) + ( 241 )

( 100 * X ^ 2 ) + ( 330 * X ) + ( 271 )

( 100 * X ^ 2 ) + ( 370 * X ) + ( 191 )

( 100 * X ^ 2 ) + ( 370 * X ) + ( 311 )

( 100 * X ^ 2 ) + ( 370 * X ) + ( 341 )

( 100 * X ^ 2 ) + ( 380 * X ) + ( 41 )

( 100 * X ^ 2 ) + ( 380 * X ) + ( 281 )

( 100 * X ^ 2 ) + ( 380 * X ) + ( 341 )

( 100 * X ^ 2 ) + ( 420 * X ) + ( 121 )

( 100 * X ^ 2 ) + ( 420 * X ) + ( 361 )

( 100 * X ^ 2 ) + ( 420 * X ) + ( 421 )

( 100 * X ^ 2 ) + ( 430 * X ) + ( 311 )

( 100 * X ^ 2 ) + ( 430 * X ) + ( 431 )

( 100 * X ^ 2 ) + ( 430 * X ) + ( 461 )

( 100 * X ^ 2 ) + ( 470 * X ) + ( 101 )

( 100 * X ^ 2 ) + ( 470 * X ) + ( 401 )

البته همان طور که مشاهده می کنید این معادلات هم , مانند معادلات غربال گر مربوط به اعدادی با یکان (9) , همگی دارای قالبی تقریبا یکسان بوده و همچنین می توان آنها را در چهار دسته کلی از نظر ضریب مولفه میانی موجود در این معادلات که به صورت کلی برابر با 120X , 130X , 170X , 180X , 220X و ... می باشند دسته بندی نمود و چون این معادلات بخش بسیار بزرگی از اعداد دارای یکان (1) را به طور کامل نسبت به وجود اعدادی که به اعداد اولی با یکان (3) و یکان (7) بخش پذیر هستند را غربال می کند آنها را معادلات غربال گر (7*3) می نامیم.

با بررسی معادلات غربال گر (3*3) و (7*7) که مربوط ساختار اعدادی با یکان (9) بوده و نیز معادلات غربال گر (7*3) که مربوط به ساختار اعدادی با یکان (1) می باشند در می یابیم چنانچه تعداد این گونه از معادلات نامتناهی باشد در نتیجه با افزایش اعداد در دو مجموعه بزرگ اعداد با یکان (1) و اعداد با یکان (9) , میزان پوشش دهی این معادلات در ساختار اعدادی با یکان (1) و یکان (9) هم افزایش می یابد به گونه ای که مثلا به ندرت می توان اعداد بسیار بزرگی با یکان (9) را یافت که با وجود عدم بخش پذیری به اعدادی با یکان (3) و اعدادی با یکان (7) , نتوان آنها را در خروجی یکی از معادلات غربال گر (3*3) و (7*7) مشاهده نمود و چون تمامی اعداد اول به طور کامل دارای ویژگی عدم بخش پذیری می باشند بنابراین اکثر اعداد اول بزرگ دارای یکان (1) و یکان (9) را می توان در خروجی های این معادلات مشاهده نمود که به دلیل وجود ضرایب کاملا متفاوت در مولفه میانی معادلات غربال گر مربوط به ساختار اعدادی با یکان (9) نسبت به معادلات غربال گر مربوط به ساختار اعدادی با یکان (1) می توان نتیجه گرفت که اعداد دوقلویی با یکان (1) و یکان (9) که اختلافشان برابر با دو واحد می باشد , تعدادشان به طور محسوسی کاهش می یابد ولی در عین حال خواهیم دید که اعداد دوقلویی که هر دو دارای یک نوع یکان , مثلا هر دو دارای یکان (9) یا هر دو دارای یکان (1) می باشند به صورت اعداد دوقلویی که اختلاف آنها اعدادی به صورت 30 , 60 , 90 , 120 و ... و به طور کل مضاربی از عدد (30) می باشند به صورت تقریبا مشخص و نامتناهی در ساختار اعداد وجود خواهند داشت و به عبارتی می توانیم به راحتی اعداد نیمه اول دوقلو با یکان (1) یا (9) را به طور حساب شده توسط این معادلات تولید نماییم که این مسئله یکی دیگر از کاربردهای معادلات غربال گر می باشد. بنابراین این معادلات می توانند بسیاری از قضایای مربوط به ساختار اعداد نظیر قضیه اعداد دوقلو و نمودار مارپیچی اولم و ... را به راحتی تحلیل و نمایش دهند که البته دلایل به وجود آمدن چنین ویژگی هایی در این معادلات به طور کامل قابل تحلیل و اثبات بوده و امیدوارم بتوانم در آینده این موضوع را که به صورت نمایشی بسیار زیبا و شگفت انگیز در مورد ساختار اعداد می باشد را در مقاله ای دیگر شرح دهم.

اطلاعات منابع مقاله :

نویسنده و نظریه پرداز مقاله : حسین اختر محققی

تاریخ انتشار مقاله : 1392/7/1

پست الکترونیکی : [e-mail]